Optimal Bet Size Using Kelly Criterion

TLDR: When placing a wager, choosing a bet size is as important as an edge. Kelly Criterion is a simple formula that determines the bet size for the highest growth in repeated games. I made a calculator/simulator to play out alternative strategies.

Suppose I offered you to play a game where we flip coins using a fair coin. If it lands on tails, you lose $1, but if it lands on heads, you win $1.02. Surely you’d play. But how much would you wager on each flip?

Before we get to that, let’s calculate the expected payout of such a game. 50% of the time you’ll make $1.02 and 50% of the time you’d lose $1.

E = 0.5 * 1.02 + 0.5 * -1 = 0.01

You’d be expecting to make $0.01 on each coin flip.

Here’s a python function that can serve as the game:

For the scenario above, the start would be 100, prob_win would be 0.5, payout_perc would be 1.02 and let’s pick a seed of 42. We just have to choose a wager_perc and num_turns. For num_turns , let’s assume we can always play this game so just pick a large number, like 1 million.

Below is a helper function that wraps up the play function so we can alter just the wager_perc and seed :

def game1(wager_perc, seed):
    return play(
        bankroll = 100,
        wager_perc = wager_perc,
        prob_win = 0.5,
        payout_perc = 1.02,
        num_turns = 1000000,
        seed = seed
    )

wager_perc is what we’re really solving for. Let’s just pick a number, like 3%.

game1(wager_perc = 0.03, seed = 42)

> 3.700281203030123e-63

Not only did we not make any money, we lost all our money. The only reason we didn’t go bust is that we didn’t set a minimum bet size, but we effectively have $0. It could have been the seed. Let’s try the first ten seeds:

print("seed\t ending balance")
for seed in range(0, 10):
    out = game1(wager_perc = 0.03, seed = seed)
---------------------------------
seed	 ending balance
0	 3.0739016765737524e-79
1	 3.4882833267497586e-56
2	 2.144222002800966e-64
3	 9.763987869593283e-60
4	 3.4739495942979628e-74
5	 3.071792897590687e-82
6	 3.2749187920734726e-67
7	 1.486847791315467e-75
8	 5.3204266409249104e-65
9	 5.655402982815484e-63

We lost money in every scenario, despite having an edge. Here’s where optimal bet size comes into play.

Enter Kelly Criterion. As per Wikipedia

[Kelly Criterion] is a formula for bet sizing that leads almost surely to higher wealth compared to any other strategy in the long run (i.e. approaching the limit as the number of bets goes to infinity)

The great thing about the formula is that its very simple and there are some shortcuts that can be made with even odd bets.

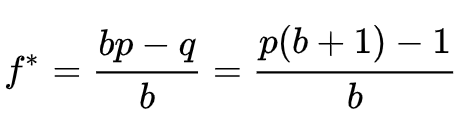Kelly CriterionKelly Criterion

  • f * is the fraction of the current bankroll to wager, i.e. how much to bet

  • b is the net odds received on the wager (“b to 1″); in the example above, it would be 1.02

  • p is the probability of winning

  • q is the probability of losing, which is 1 − p

So in the example above, the Kelly Criterion formula would be

payout_perc = 1.02 # b above
prob_win = 0.5  # prob win # p above

def kelly(prob_win, payout_perc):
    return (prob_win * payout_perc - (1 - prob_win)) / payout_perc

Let’s see how it does

seed	 ending balance
0	 3.5344345382967407e+19
1	 1.1996567561250315e+27
2	 2.493886480093249e+24
3	 8.28892500677546e+25
4	 1.5808564995340084e+21
5	 3.700773593802014e+18
6	 2.999344683799298e+23
7	 5.6475800476424215e+20
8	 1.5818010128591278e+24
9	 7.262735004222799e+24

That’s a big difference.

Let’s try some other values:

kelly(prob_win=0.50, payout_perc=1) # 0
kelly(prob_win=0.51, payout_perc=1) # 0.02
kelly(prob_win=0.52, payout_perc=1) # 0.04

If you have no edge, the optimal bet size would be 0. You may notice a pattern too where if you have an even-money bet (i.e. payout percent 1), you should bet twice your edge. For instance, if you have a 51% odds of winning, your edge is 1%, so you should bet 2% of your bankroll on each turn.

Conclusion and Caveats

Should you use Kelly Criterion?

Yes? I suppose it depends on what you’re using right now. In practice, many practitioners use as a rule of thumb of 50% optimal bet size to account for uncertainty in their probability and payout estimations.

It also depends on your personal risk preference and how willing you are to be down, even with the odds in your favor. For instance, if you have even odds with a 60% probability of winning, Kelly Criterion would tell you to gamble 20% of your payroll. But if you lose 3 times in a row (6.4% chance), you’d be down nearly 50%. You might not have the stomach to keep going.

The other thing to consider is that Kelly Criterion assumes you can play an infinite number of times. If the expected value is greater than zero and you have one shot, you would be better off betting everything, assuming you’re not adverse to losing all your money. If you had an infinite number of chances, then you should use Kelly Criterion. But in most decisions we make, we have a finite number of chances to play.

Take for instance a game in which we have even payout and 52% chance of winning. Kelly Criterion says our optimal wager would be 4% and Using the simulator I made, we can see that a simulation of 10 games with 100k steps, our Kelly payout beats 8% wager in all factors.

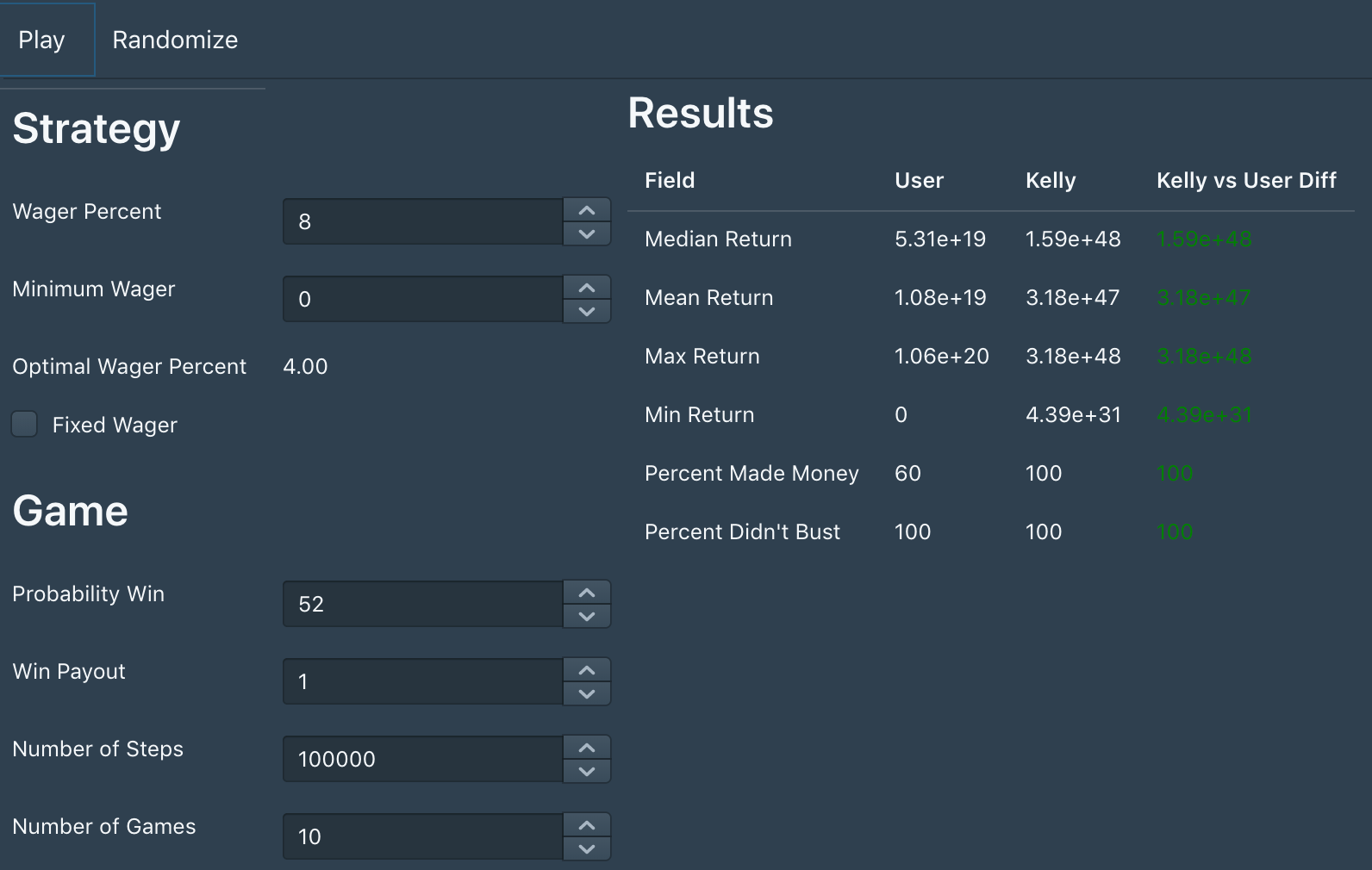Simulated 10 games with 100k steps, 52% probability winning, even odds, over-aggressiveSimulated 10 games with 100k steps, 52% probability winning, even odds, over-aggressive

But suppose we had a game of only 100 steps (note I set the number of games to 100k to get a more representative sample).

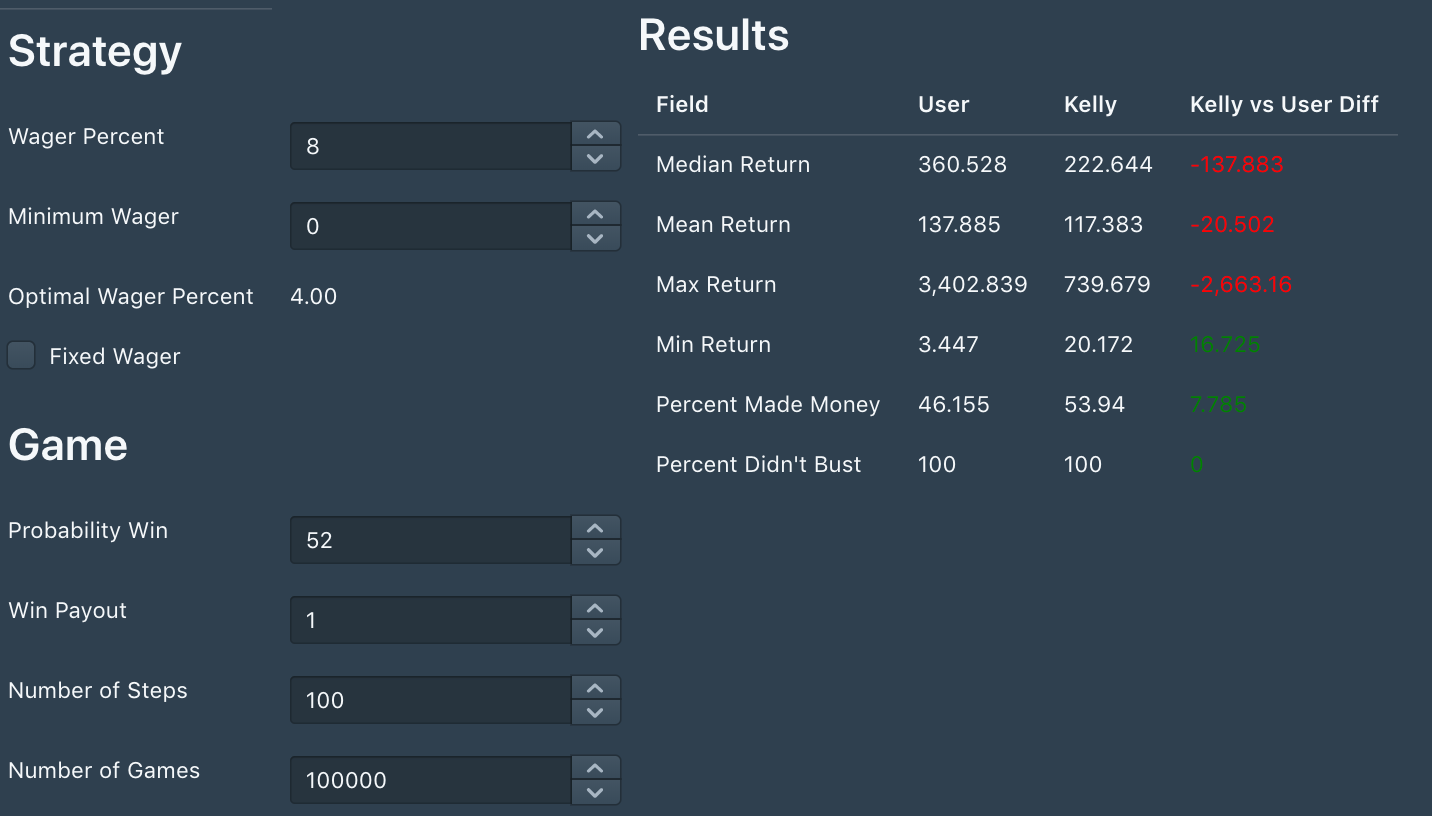Simulated 100000 games with 100 steps, 52% probability winning, even odds, over-aggressiveSimulated 100000 games with 100 steps, 52% probability winning, even odds, over-aggressive

Now the results are not so clear. Our median and mean return are significantly higher playing with an 8% wager strategy (360 vs 222 and 137 vs 117, respectively). However, the minimum return is lower and the strategy only made money 46% of the time opposed to 53% of the time.

So if we had one shot to play a positive expected value game we’d choose 100% wager, and if we had an infinite number of times to play, we’d choose Kelly, then if we had some finite number of times to play we should choose something in-between (pushing us to a more aggressive strategy). This counteracts the factor above that pushes us towards a more conservative strategy, but its worth pointing out.

There are some researchers that tried to adjust the formula for a finite number of games, but as a rule of thumb, Kelly’s Criterion can help us make wise decisions when dealing with games of chance.