Floating point number representations are annoying to work with. Lisp and by extension Clojure deal with them by using fractions instead.
Floating point representations can lead to some strange results. Lisp and Clojure have fraction representations built in, helping avoid many of the problems with floats.
I came across this article about why the IRS has had trouble to break away from Cobol. The article argues that a big reason is due to Cobol’s native support of fixed point as opposed to floating point. Below is a quick recap of the article and the problem with floating points.
The problem with floating point representation
The nature of floating point representations results in some unexpected values. For instance, in python if you try to add 0.1 and 0.2 you get the result below.
>>> 0.1 + 0.2
0.30000000000000004
The dangerous thing about this is that it crops up in unexpected places and during recursion can build up to drastically deviate from the expected result. Muller’s Recurrence is a prime example.
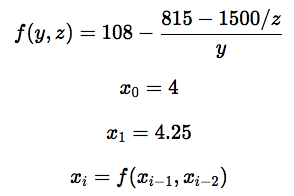
Example of Muller’s Recurrence
If you were to compare the results as i goes from 0 to 19 using floating vs fixed points, you would get the results below.
i | floating pt | fixed pt
-- | -------------- | ---------------------------
0 | 4 | 4
1 | 4.25 | 4.25
2 | 4.47058823529 | 4.4705882352941176470588235
3 | 4.64473684211 | 4.6447368421052631578947362
4 | 4.77053824363 | 4.7705382436260623229461618
5 | 4.85570071257 | 4.8557007125890736342039857
6 | 4.91084749866 | 4.9108474990827932004342938
7 | 4.94553739553 | 4.9455374041239167246519529
8 | 4.96696240804 | 4.9669625817627005962571288
9 | 4.98004220429 | 4.9800457013556311118526582
10 | 4.9879092328 | 4.9879794484783912679439415
11 | 4.99136264131 | 4.9927702880620482067468253
12 | 4.96745509555 | 4.9956558915062356478184985
13 | 4.42969049831 | 4.9973912683733697540253088
14 | -7.81723657846 | 4.9984339437852482376781601
15 | 168.939167671 | 4.9990600687785413938424188
16 | 102.039963152 | 4.9994358732880376990501184
17 | 100.099947516 | 4.9996602467866575821700634
18 | 100.004992041 | 4.9997713526716167817979714
19 | 100.000249579 | 4.9993671517118171375788238
For more discussion, visit the original article. It goes more in depth and I recommend reading it.
Muller’s Recurrence in Clojure
I’ve been dabbling in lisp and Clojure over the last few weeks (Clojure is a dialect of lisp). One of the cool things about lisp is that it handles fractions natively. For example, when doing integer division the results are represented as fractions. 1 divided by 10 is the fraction 1/10. And operations on fractions work as expected.
(/ 1 10) => 1/10
(+ 1/10 2/10) => 3/10
Of course you can still do floating point calculations.
(/ 1 10.0) => 0.1
(+ 0.1 0.2) => 0.30000000000000004
As a quick side-note, lisp has a syntax different from most modern programming languages.
Most languages:
function(arg1, arg2, ..., argn)
e.g. sum(1, 2)
Lisp
(function-name arg1 arg2 ... argn)
e.g. (sum 1 2)
In general, lisp handles numbers very well and can do some impressive calculations. Below is an example of 53 ^ 53 in Common Lisp (example stolen from the great book Land of Lisp).
> (expt 53 53)
24356848165022712132477606520104725518533453128685640844505130879576720609150223301256150373
Muller’s Recurrence in Clojure
How would the previous example of Muller’s Recurrence look in Clojure?
(defn rec
[y,z]
(- 108
(/
(- 815
(/ 1500 z))
y)
))
The above defines a function rec, which takes two parameters, y and z. Again, here is the formula we used as an example of Muller’s Recurrence.
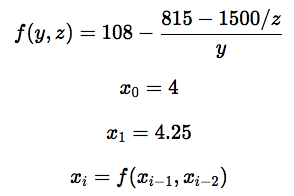
Muller’s Recurrence
To calculate xi recursively, we can use the formula below, which will print out our results as they get processed.
(defn recn
[n y z]
(do (println n y z)) (if (<= n 0) z (recn (- n 1) (rec y z) y)))
Since Clojure works with fractions, using fractions as inputs just treats everything as a fraction, avoiding the problem with floating points.
=> (recn 20 17/4 4)
20 17/4 4
19 76/17 17/4
18 353/76 76/17
17 1684/353 353/76
16 8177/1684 1684/353
15 40156/8177 8177/1684
14 198593/40156 40156/8177
13 986404/198593 198593/40156
12 4912337/986404 986404/198593
11 24502636/4912337 4912337/986404
10 122336033/24502636 24502636/4912337
9 611148724/122336033 122336033/24502636
8 3054149297/611148724 611148724/122336033
7 15265963516/3054149297 3054149297/611148724
6 76315468673/15265963516 15265963516/3054149297
5 381534296644/76315468673 76315468673/15265963516
4 1907542343057/381534296644 381534296644/76315468673
3 9537324294796/1907542343057 1907542343057/381534296644
2 47685459212513/9537324294796 9537324294796/1907542343057
1 238423809278164/47685459212513 47685459212513/9537324294796
0 1192108586037617/238423809278164 238423809278164/47685459212513
238423809278164/47685459212513
Note this example counts down from 20 while the original example counts up to 20.
If we want to convert that final value to a float, we can do so:
(float **238423809278164/47685459212513**)
4.9999268795046
But of course, if you start out with floats, you’ll have the same problem:
=> (recn 20 4.25 4)
20 4.25 4
19 4.470588235294116 4.25
18 4.6447368421052175 4.470588235294116
17 4.770538243625083 4.6447368421052175
16 4.855700712568563 4.770538243625083
15 4.91084749866063 4.855700712568563
14 4.945537395530508 4.91084749866063
13 4.966962408040999 4.945537395530508
12 4.980042204293014 4.966962408040999
11 4.987909232795786 4.980042204293014
10 4.991362641314552 4.987909232795786
9 4.967455095552268 4.991362641314552
8 4.42969049830883 4.967455095552268
7 -7.817236578459315 4.42969049830883
6 168.93916767106458 -7.817236578459315
5 102.03996315205927 168.93916767106458
4 100.0999475162497 102.03996315205927
3 100.00499204097244 100.0999475162497
2 100.0002495792373 100.00499204097244
1 100.00001247862016 100.0002495792373
0 100.00000062392161 100.00001247862016
100.00001247862016
Lisp’s native handling of fractions is a nice feature that can help you avoid some problems associated with floating point numbers.
By Branko Blagojevic July 30, 2018