A recent EconTalk podcast featured Nassim Taleb in which he spoke about his new book Skin in the Game. During the discussion, he criticized…
A recent EconTalk podcast featured Nassim Taleb in which he spoke about his new book Skin in the Game. During the discussion, he criticized behavioral economists and social scientists for designing “one-shot” type experiments and trying to draw real life insights from the results. When in actuality, the more reasonable scenario is a series of interactions.
For instance, an experiment may look at your willingness to wager on an event and how that changes over time. And what some studies have shown is that people increase risk seeking in the presence of prior gains. The is called the “house money effect”. The idea is that you’re essentially playing with the house’s money (rather than your own), so you’re less risk averse. These findings are normally attributed to illogical biases, leftover remnants of human nature that we just can’t seem to shake. Why should you treat your recently won money any different than that which you had from earlier?
But Taleb sees it differently. He believes much of what is believed by social scientists to be illogical human biases make sense when you consider the game as a series of interactions. He brings this around to the idea of survival and introduces the idea of absorbing barriers:
Taleb: … absorbing barrier is a point that you reach beyond which you can’t continue. You stop. So, for example, if you die, that’s an absorbing barrier. So, most people don’t realize, as Warren Buffett keeps saying, he says in order to make money, you must first survive. It’s not like an option. It’s a condition. So, once you hit that point, you are done. You are finished. And that applies in the financial world of course to what we call ruin, financial ruin.
So being more risk averse with money won makes sense in this context. If you value financial survival above all else, then naturally you would be less willing to bet your last dollar than your recently won earnings.
Taleb: Exactly. Behavioral economists have something called mental accounting, which states exactly what you just said: that treating money according to the source is irrational because these are one-period models. That’s how they view the world, as a one-shot experiment. They don’t view the world as repetition. A repetition of bets. So, if you look at the world as repetition of bets, under condition of survival, then mental accounting is not only not irrational but is necessary. Any other strategy would be effectively irrational.
But he goes one step farther. He says on a long enough time scale, as long as you have an absorbing barrier (e.g. no capital left to wager or death), then you will end in ruin unless you engage in these types of strategies. This is true even if you have the edge.
Taleb: … Actually, what I’m saying is even stronger. I am saying that even if you have the edge, in the presence of the probability of ruin, you will be ruined. Even if you had the edge … If you play long enough. Unless you engage in strategies designed by traders and rediscovered by every single surviving trader, very similar to what we call, something called the Kelly Criterion, which is to play with the house money. In other words, you start betting in a casino, the strategy is as follows: You go with $100, whatever you want; and you bet $1. If you lose your bet less than a dollar, you bet, say, 90 cents, or whatever; and if you make money, you start betting with the house money. And this is called, playing with the market money or playing with the house money. And so increase your bet as you are making money, and you reduce your bet as you are losing money. And that strategy is practically the only one that allows you to gamble or engage in risky strategy without ruin.
Normally we think about it the other way around. If we have a slight edge, we should just keep playing and in the long run, we’re better off since we have the edge. But what Taleb is saying is in the presence of absorbing barriers, we’ll eventually hit ruin using a naive strategy.
This makes sense in a way since on a long enough time scale we’re all dead. Also, randomness doesn’t behave as people normally expect and long runs are more common than we anticipate.
I had a professor in class tell us all to flip a coin 100 times and record the results, or just cheat and put down 100 random head/tail values. After we had done so, he would walk around and tell us whether we cheated or not. The way he could tell would be by looking if we have a string of 8 heads (or tails) values in a row. Such a string in 100 trials is much more likely than most people give credit for. Sure enough…
import numpy as np
np.random.seed(42)
np.random.randint(2,size=100)
array([0, 1, 0, 0, 0, 1, 0, 0, 0, 1, 0, 0, 0, 0, 1, 0, 1, 1, 1, 0, 1, 0, 1, 1, 1, 1, 1, 1, 1, 1, 0, 0, 1, 1, 1, 0, 1, 0, 0, 0, 0, 0, 1, 1, 1, 1, 1, 0, 1, 1, 0, 1, 0, 1, 0, 1, 1, 0, 0, 0, 0, 0, 0, 0, 0, 1, 1, 0, 1, 1, 1, 1, 0, 1, 0, 1, 1, 1, 0, 1, 0, 1, 0, 1, 0, 0, 1, 0, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 0])
I wanted to test Taleb’s idea of dynamic strategies in games of chance. Rather than diving into the math, I just setup experiments. Below are a few functions that help me test various strategies.
From this, we can vary the payout as well as the strategy based on the capital we have.
To start out with, I looked at even payouts of [-1, 1], bet size is set to a constant value of 1, capital of 100, over 100 individuals and max number of steps 1,000,000, so it doesn’t run too long.
payout_50_50 = create_payout([-1,1], [0.5, 0.5], seed=42)
same_bet = lambda x: 1
payout_50_50_results = test(payout=payout_50_50, strategy=same_bet, num_trials=100, start_capital=100, max_num_steps=100000)
display_results(payout_50_50_results)
Number of individuals still alive: 25 (25%)
Number of steps alive:
10%: 4231 25%: 8037 50%: 20902 99%: 100001
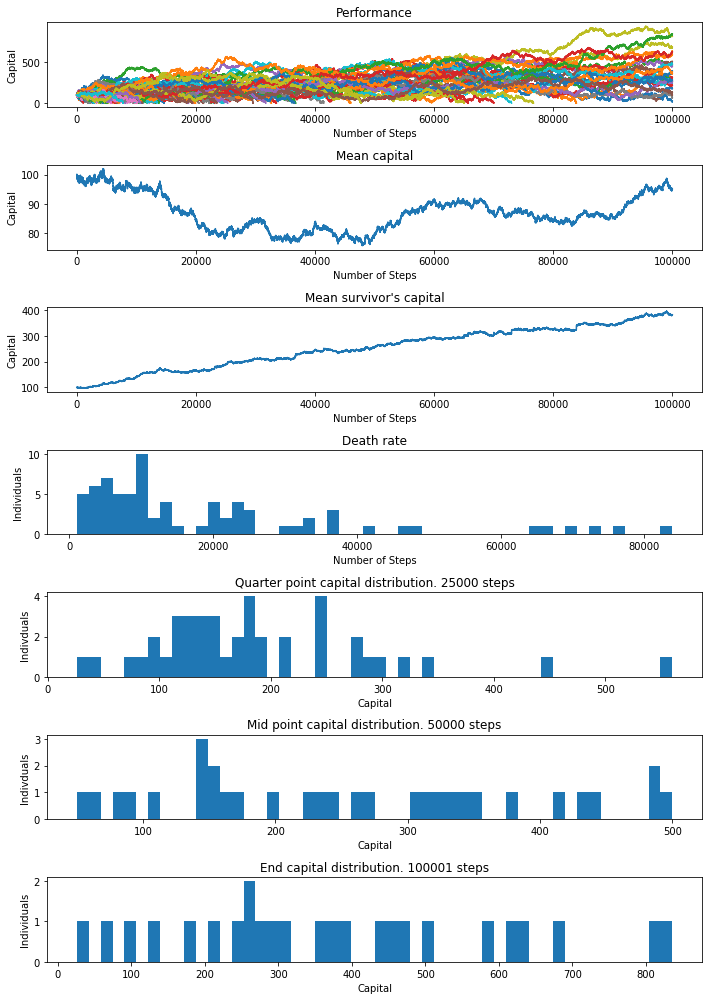
In this result, 25 individuals survived after 1MM steps. It looks like most went bust rather early. But a few went bust even later in the process and some have low capital so letting it run longer would likely kill everyone off. Another interesting result is that the distribution of capital is becoming less normally distributed as individuals die off.
What Taleb said is we should be more aggressive with the house money. One way to do this is to bet a constant percent of our capital (say 1%). We need to consider the minimum bet size (say 0.01) as well because without it, no one would ever die. Let’s see the results:
payout_50_50_perc = create_payout([-1,1], [0.5, 0.5], seed=42)
payout_50_50_perc_results = test(payout=payout_50_50_perc, strategy=same_perc_bet, num_trials=100, start_capital=100, max_num_steps=100000)
display_results(payout_50_50_perc_results)
Number of individuals still alive: 55 (55%)
Number of steps alive:
10%: 48865 25%: 71462 50%: 100001 99%: 100001
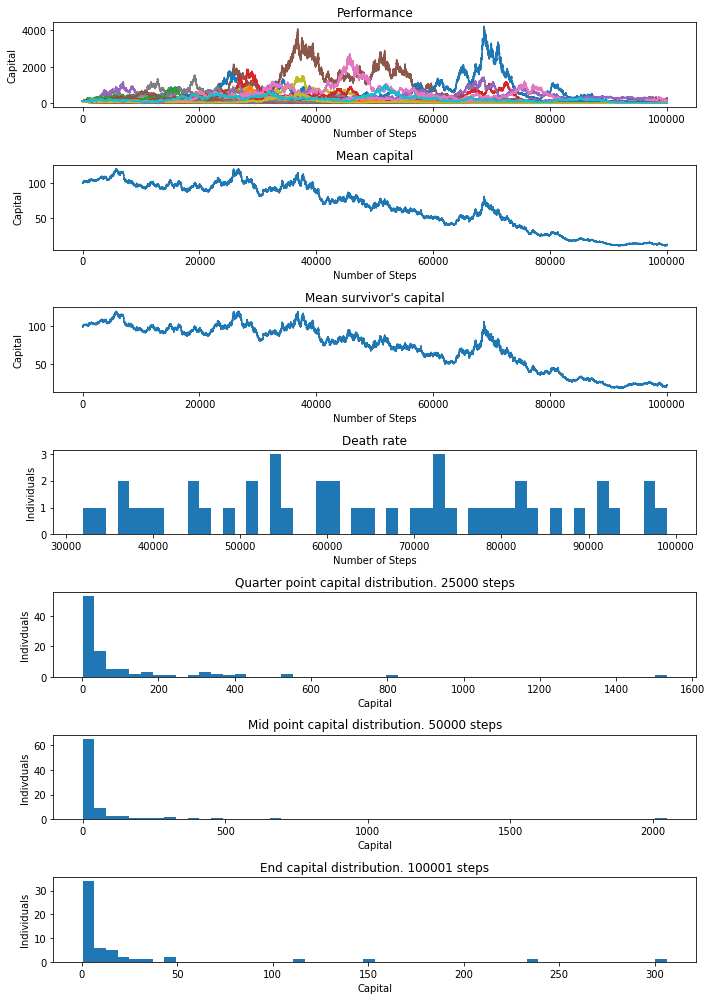
He’s right in that survival is considerably higher at 55% but overall capital is much lower and distribution of capital is much more uneven. This can be thought of as sacrificing absolute population capital for survival. Whether this is a good strategy obviously depends on how much you value survival over population capital. But it makes sense that you can’t get something for nothing with even odds.
Let’s tilt the odds just slightly at odds of winning set at 50.01%. Below are the results of the same bet
payout_4999_5001 = create_payout([-1,1], [0.4999, 0.5001], seed=42)
payout_4999_5001_results = test(payout=payout_4999_5001, strategy=same_bet, num_trials=100, start_capital=100, max_num_steps=100000)
display_results(payout_4999_5001_results)
Number of individuals still alive: 26 (26%)
Number of steps alive:
10%: 4004 25%: 7466 50%: 19455 99%: 100001
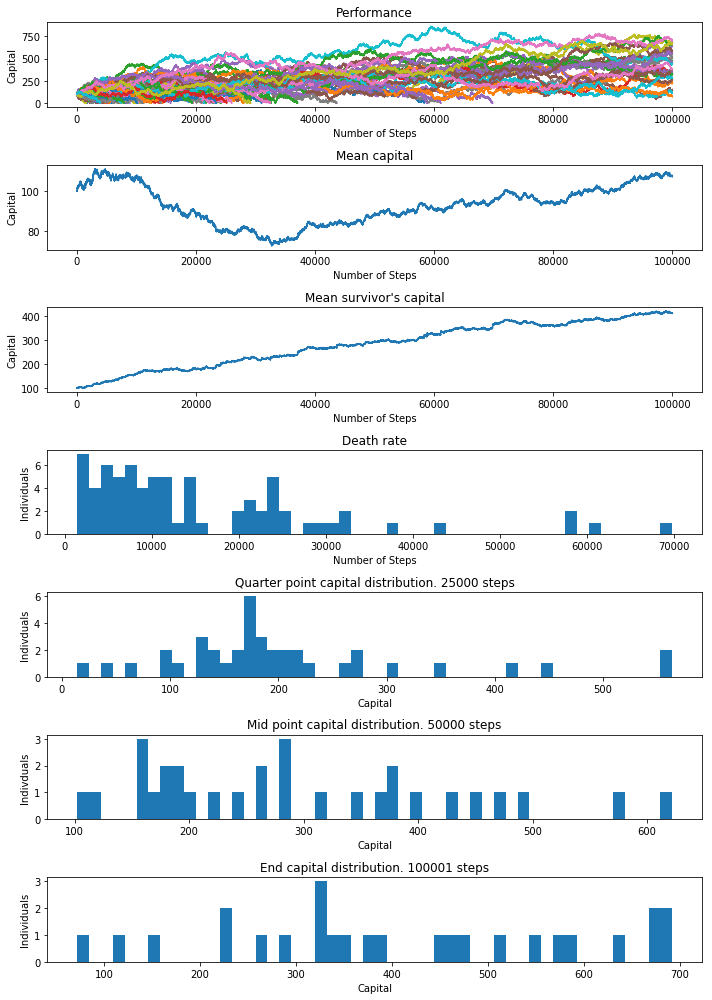
About the same survivorship as the 50/50 odds and overall capital is slightly higher towards the end, which is due to the slight odds in our favor. And deaths slow as more capital is built up by the survivors, which reduces the bet size relative to the capital.
What about if we apply a constant percentage bet with a slight edge?
payout_4999_5001 = create_payout([-1,1], [0.4999, 0.5001], seed=42)
payout_4999_5001_perc_results = test(payout=payout_4999_5001, strategy=same_perc_bet, num_trials=100, start_capital=100, max_num_steps=100000)
display_results(payout_4999_5001_perc_results)
Number of individuals still alive: 61 (61%)
Number of steps alive:
10%: 49291 25%: 71622 50%: 100001 99%: 100001
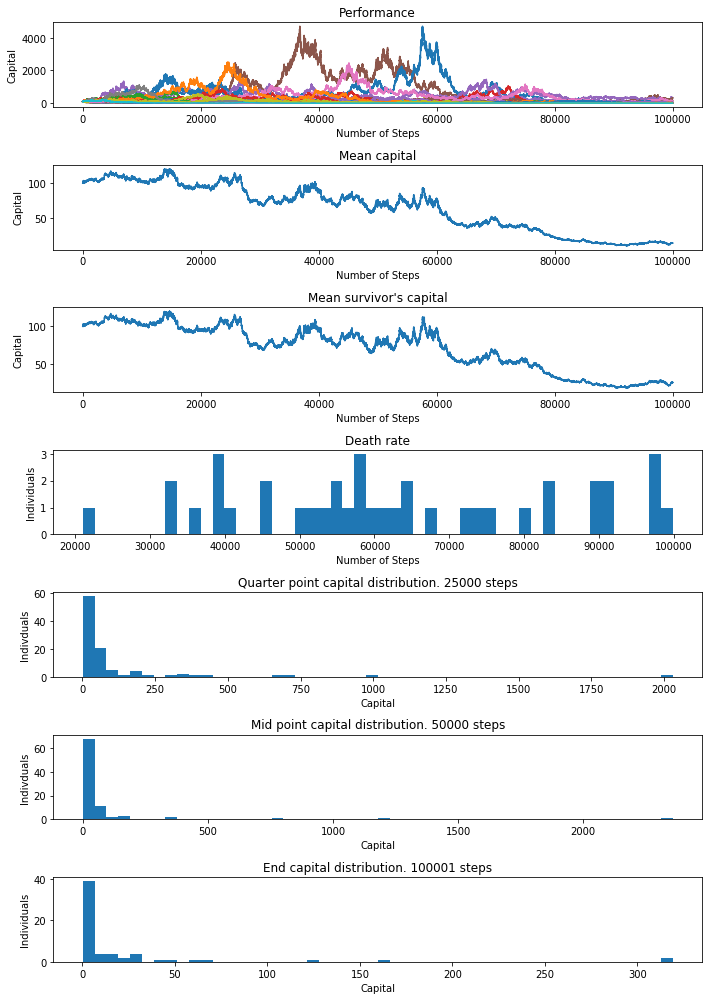
As with the percentage bet at 50/50 odds, survivorship is higher but overall capital is considerably lower and we basically gave up the edge and saw a steady decline in capital of both the survivors and population.
How about an edge of 1%. These are the results for the constant bet size of 1:
payout_49_51 = create_payout([-1,1], [0.49, 0.51], seed=42)
payout_49_51_results = test(payout=payout_49_51, strategy=same_bet, num_trials=100, start_capital=100, max_num_steps=100000)
display_results(payout_49_51_results)
Number of individuals still alive: 100 (100%)
Number of steps alive:
10%: 100001 25%: 100001 50%: 100001 99%: 100001
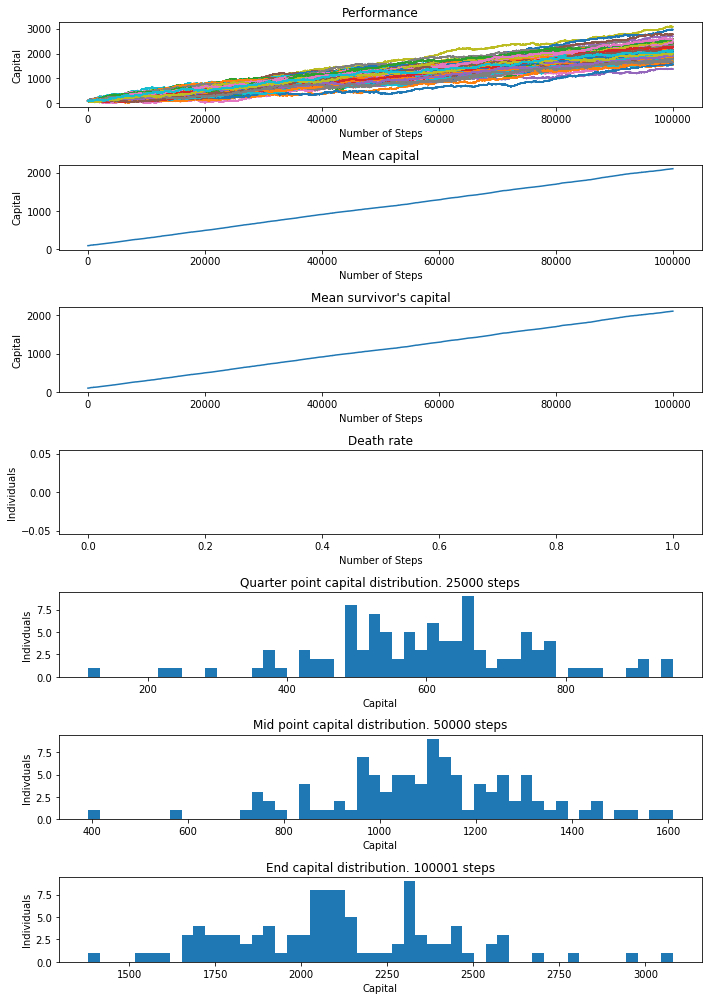
I guess 1% edge was enough to keep everyone alive long enough. If you run this forever, maybe some individuals would die, but after 1MM steps, all individuals have enough capital and the bet size is so small that I don’t think they’d die for a long time. Also, notice that capital skews a bit towards the end, but it’s not crazy.
How about constant 1% bet with a 1% edge?
payout_49_51_perc = create_payout([-1,1], [0.49, 0.51], seed=42)
payout_49_51_perc_results = test(payout=payout_49_51_perc, strategy=same_perc_bet, num_trials=100, start_capital=100, max_num_steps=100000)
display_results(payout_49_51_perc_results)
Number of individuals still alive: 100 (100%)
Number of steps alive:
10%: 100001 25%: 100001 50%: 100001 99%: 100001
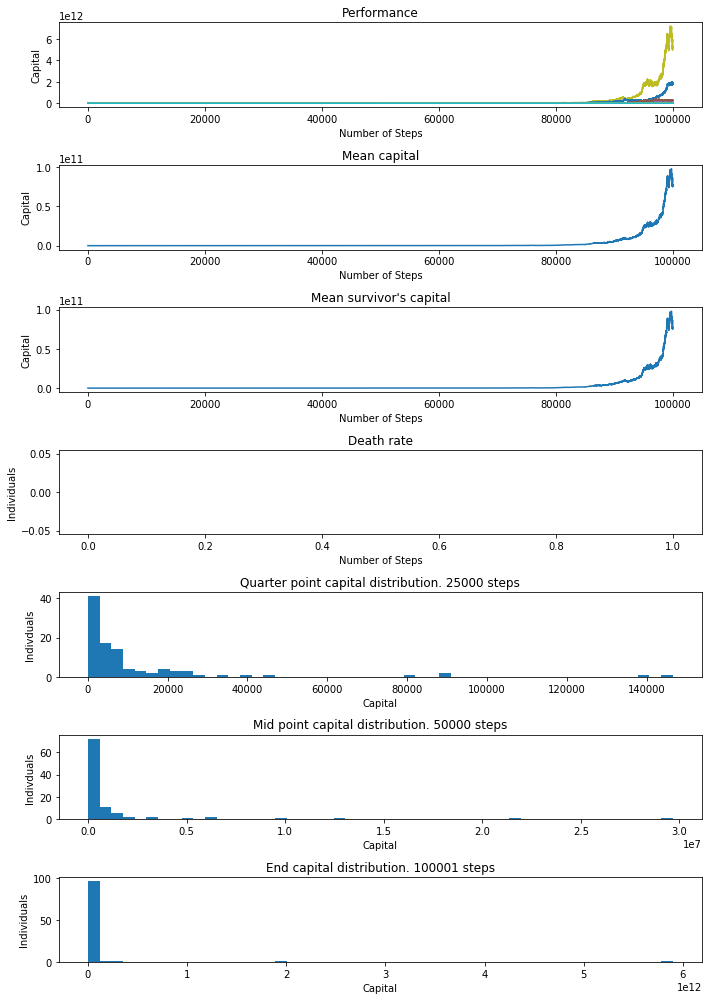
No ones dies and capital is significantly larger, although the capital becomes unevenly distributed early on and only gets worse over time. As long as you don’t mind inequality of capital distribution, this method produces the greatest wealth for the population.
So there exists some point X between 0.5001 and 0.51 in which the constant percent bet strategy begins to dominate the constant bet size strategy.
There may be other ways to varying risk tolerance with the house money. Betting a constant percent of wealth is a very simple naive approach, but you can probably apply a fancy log function to your wealth or cap or floor your max bet. But no matter what, you can’t get something for nothing. There is no strategy to beat even odds
The main considerations are how much you value survival over performance and whether you have a large enough edge or not. If you have a considerable edge, then a constant percent bet is great for performance and survival. If its even odds or only a slight edge, a constant percent will help with survival at the expense of capital growth of the population.
Discussion on hacker news.
By Branko Blagojevic on March 7, 2018
